Two-way ANOVA examines main effects and interactions, by partitioning the variance as follows:

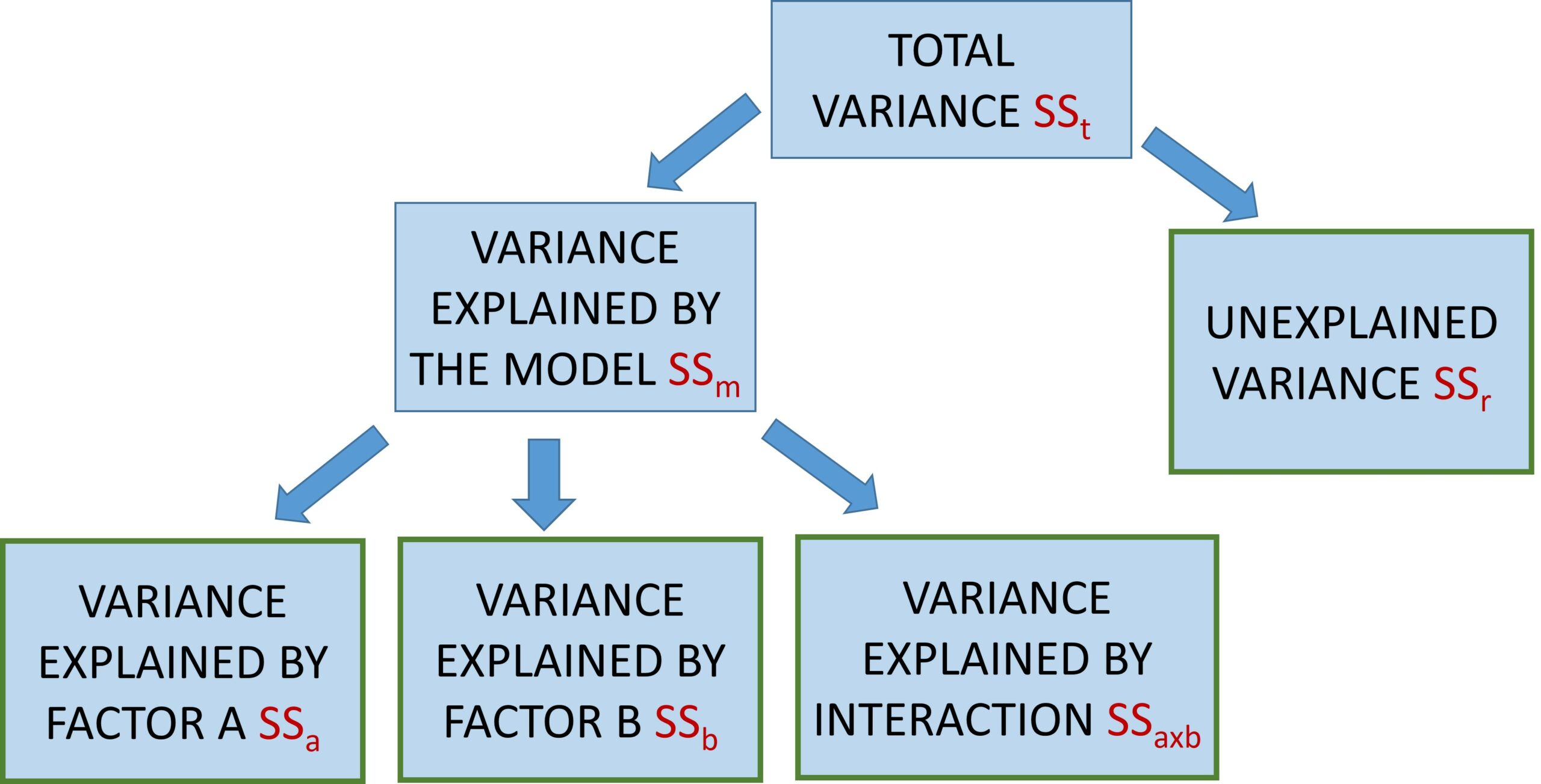
With a two-way ANOVA, we will therefore be computing three F‘s, one for each main effect (main effect of factory A, main effect of factor B) and one for the interaction (A x B).

Thus, a factorial ANOVA allows us to examine both main effects and interactions.

Main Effects

Main effects compare marginal means. The marginal means represent the means of the levels of each variable while collapsing across the levels of the other variable.

In a two-way design (i.e., with two factors/independent variables), there are two possible main effects – one for each factor. In a three-way design (i.e., with three factors) there are three possible main effects).

Interactions

Interactions occur when the effect of one factor depends on or changes according to the levels of the other factor. For example, perhaps the effect of time of day on students’ memory for class material depends on caffeine intake. When students consume placebo, we might see a strong effect of time of day, whereby students who sit in the morning lecture later remember much more than students who sit in an afternoon lecture. On the other hand, when students consume caffeine before class, we might see a weak effect or even no effect of time of day: the caffeinated students might perform equally well in the morning and the afternoon class. Therefore, we would say that there is an interaction between time of day and caffeine intake: how time of day impacted students’ performance depended on whether or not they were caffeinated!

The most helpful way to understand what a significant interaction means (or to write about a hypothesized interaction) is to graph the data (or sketch a graph of what you expect). We usually do this by putting one independent variable on the x-axis and then indicating the other independent variable by using different coloured lines or bars. If you have a significant interaction, your lines will not be parallel (note that you could have a non-significant interaction even with non-parallel lines!). In class, we shall break this down in more detail and you practice describing an interaction when you have a significant interaction in your data.

Types of Interactions

An interaction is called an ordinal interaction when the lines do not cross. In this case, the effect of factor A may be present for both levels of factor B, but the effect may be lessened for one of the levels. Or, the effect of factor A may be present for just one level of factor B. In the first instance, the main effect of factor A may still be meaningful. In the second case, it may not be useful to talk about a main effect of factor A, because that main effect is only present for one level of factor B. On the other hand, when we have a disordinal interaction, then the lines cross and it may be that the effect of factor A is opposite for the two levels of factor B. We would still report the results of the main effects, but it would only be meaningful to interpret the interaction, since this qualifies the main effects. We shall look at examples of these in class.

Try sketching what an ordinal interaction and a disordinal interaction might look like for our 2 x 2 time of day (morning or afternoon) and caffeine intake (placebo or one dose of caffeine) example.

Interpreting Interactions: Simple Main Effects

We can use a further statistical test, called simple main effects, to break down interactions. Simple main effects test the effect of one independent variable at each level of the other independent variable. For example, let’s say we were looking at the effect of time of day (morning, afternoon, or evening) and caffeine intake (placebo vs. one dose of caffeine) on memory for lecture material. If we obtained a significant interaction between time of day and caffeine intake, we could run simple main effects to find out if there is a significant effect of time of day for the placebo dose, and for the one dose of caffeine, separately. Simple main effects are not available in the regular ANOVA package in jamovi, but they are available in the gamlj (linear models) add-on. These are beyond the scope of this class, but if you need them in future, you will know where to find them!

Interpreting Interactions: Planned Comparisons or post hoc Tests

Just as we did with our one-way ANOVA, we can also explore interactions further using planned comparisons (when we have specific a priori predictions about which pairs of cell means will differ from each other) or post hoc tests (if we had no a priori predictions).

It can be a little clunky to do this in jamovi. For planned comparisons, you can select to do Contrasts, but these will just break down the main effects and not a significant interaction. You can select an interaction term and run post hoc tests on the interaction term. This will compare all possible pairs of cell means. However, note that we should not compare cell means that are confounded (i.e., that differ on more than one factor). If we get a difference when we look at a confounded comparison, we won’t know if the difference is due to factor A or factor B! Therefore, we only look at unconfounded comparisons, where the cell means differ only along one factor. As in chapter 6, we can also use the method of looking at a subset of the post hoc tests (and applying our own correction for multiple comparisons) as a work around to get planned comparisons (assuming we actually had a priori predictions!).

This starts to get a bit mind-boggling, so we shall look at some specific examples in class.

Interpreting Interactions: What If the Interaction Was Not Significant?

If you predicted an interaction and were hoping to run some planned comparisons to describe it, but the interaction is not significant when you run the ANOVA you should not then run the planned comparisons. We shall look at an example like this in chapter 9.