1. Look at the Data

Let’s run an example with data from lsj-data. Open data from your Data Library in “lsj-data.” Select and open “Broca’s aphasia.”

This dataset contains hypothetical data in which six patients suffering from Broca’s Aphasia (a language deficit commonly experienced following a stroke) completed three word recognition tasks. On the first (speech production) task, patients were required to repeat single words read out aloud by the researcher. On the second (conceptual) task, designed to test word comprehension, patients were required to match a series of pictures with their correct name. On the third (syntax) task, designed to test knowledge of correct word order, patients were asked to reorder syntactically incorrect sentences. Each patient completed all three tasks. The order in which patients attempted the tasks was counterbalanced between participants. Each task consisted of a series of 10 attempts. The number of attempts successfully completed by each patient are provided in the dataset.

Data Set-Up

To conduct the repeated measures ANOVA, we first need to ensure our data is set-up properly in our dataset. This requires multiple columns, one for each condition or time measurement, with the values indicating the measurement of the DV for that condition or time. Each row is a unique participant or unit of analysis.

So for our broca dataset, we have our Participant column indicating their participant number and then one column for each of the three word recognition tasks (speech, conceptual, syntax), with their scores on the knowledge test indicating the dependent variable for each condition.

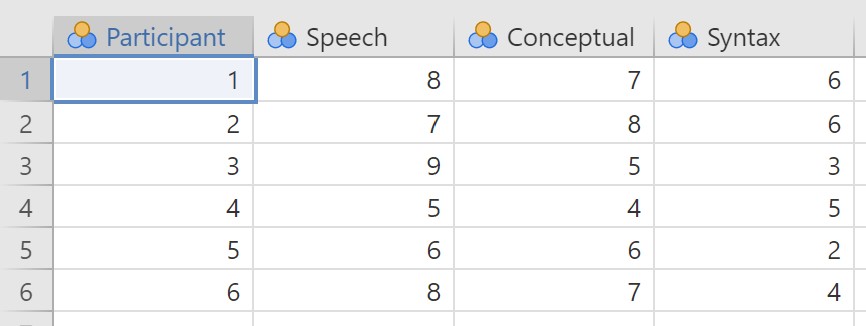
In the data above, what is your independent variable and what are the levels of the independent variable? What is your dependent variable?

Describe the Data

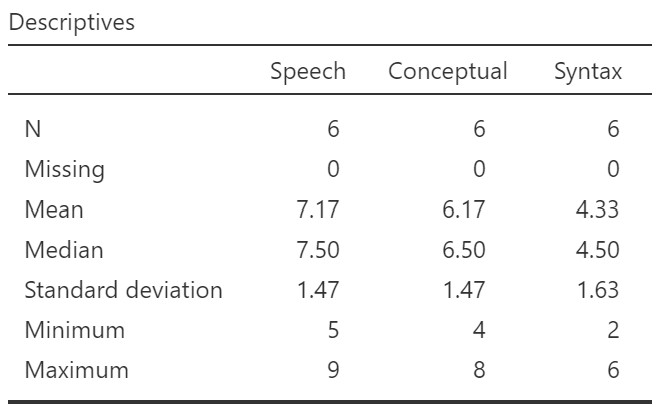
Once we confirm our data is setup correctly in jamovi, we should look at our data using descriptive statistics and graphs. First, our descriptive statistics are shown below (obtain these by going to Exploration, Descriptives, and selecting all three levels of the independent variable as “Variables.”) We see that there are only six cases total (oof, really small data set!) and the average test score on each of the three conditions. It appears participants did best on the speech condition, but we’ll need to run our repeated measures ANOVA to know for sure.

Hypotheses

Let’s say we have predicted that there is an effect of task type on word recognition scores.

2. Check Assumptions

As a parametric test, the repeated measures ANOVA has the same assumptions as other parametric tests (minus the assumption of independence, because all participants participate in all conditions):

1. The dependent variable is normally distributed
2. Variances in the two groups are roughly equal (i.e., homogeneity of variances); in repeated measures ANOVA this is called the assumption of sphericity
3. The dependent variable is interval or ratio (i.e., continuous).

To check assumptions 1 and 2, we need to run the repeated measures ANOVA in jamovi.

To begin the repeated measures ANOVA in jamovi

1. Select ANOVA, and then Repeated Measures ANOVA.
2. You now need to tell jamovi what your repeated measures “factor” (independent variable) is by specifying its names and the levels in the box called Repeated Measures Factors. Click where it says “RM Factor 1” and type the name of your independent variable (in this example, I am calling it “Task Type”). Next, rename hte three levels of task by typing Speech, Conceptual, and Syntax, where it says “Level 1,” “Level 2,” and “Level 3” below.
3. Click and drag your three variables to the Repeated Measures Cells box (or select them all by clicking on each while holding down the Shift key and click on the little arrow to move them to the Repeated Measures Cells box).

Now you can select the assumptions.

Testing Normality

We cannot test normality using all four methods we previously learned about because in this case we are checking normality of the residuals. You don’t need to know what that means yet (we’ll discuss it more when we go over regression).

To check normality for the repeated measures ANOVA, we have to go run the repeated measures ANOVA in jamovi. To test normality, under ‘Assumption Checks’ we select Q-Q plot. It is currently the only option we have available for testing normality in the repeated measures ANOVA. As with the Q-Q plot we looked at for the one-way ANOVA, we are looking for the dots to be close to the straight line.

There are alternatives to the repeated measures ANOVA if we are concerned about violating the assumption of normality (and/or when we have small sample sizes). The non-parametric equivalent is Friedman’s test (which we shall look at briefly in the next section).

Testing Sphericity

The sphericity assumption is essentially the repeated measures ANOVA equivalent of homogeneity of variances. Sphericity means there is equality of variances of the differences between treatment levels. For example, if there are three groups, then the difference in all three pairs of differences (1-2, 1-3, 2-3) need to have approximately equal variances. You only need to care about sphericity when there are at least three conditions, which is why we did not talk about this with the dependent t-test.

Fortunately, like the other assumption checks, testing for sphericity is as simple as a checkbox in jamovi. Check the box Sphericity tests under the Assumption Checks drop-down menu. That produces the following output:

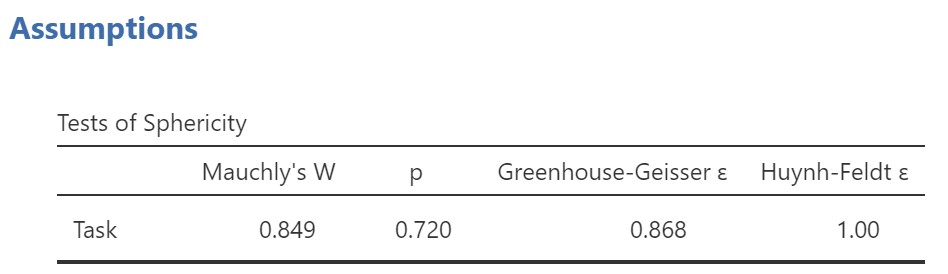
According to this output, we have not violated the sphericity assumption (because Mauchly’s test was not significant, p > .05). However, as noted earlier, we have a small sample size and so this test will be underpowered. I recommend using the Greenhouse-Geisser correction when you run the repeated measures ANOVA (see below).

3. Perform the Test

1. Select ANOVA, and then Repeated Measures ANOVA.
2. You now need to tell jamovi what your repeated measures “factor” (independent variable) is by specifying its names and the levels in the box called Repeated Measures Factors. Click where it says “RM Factor 1” and type the name of your independent variable (in this example, I am calling it “Task Type”). Next, rename the three levels of task by typing Speech, Conceptual, and Syntax, where it says “Level 1,” “Level 2,” and “Level 3” below.
3. Click and drag your three variables to the Repeated Measures Cells box (or select them all by clicking on each while holding down the Shift key and click on the little arrow to move them to the Repeated Measures Cells box).
4. Select Generalised η² (eta-squared) as your measure of effect size.
5. Rename your Dependent Variable Label to match what is being measured across all conditions or time points. In this case, in the three conditions we are measuring their scores on the word recognition task. I will just call this “Word recognition score.”
6. Under Assumption Checks, select Sphericity tests, and, for illustrative purposes, select all three boxes under the Sphericity corrections.
7. Under Post Hoc Tests, move Task Type to the box on the right and select the Holm correction.
8. Under the Estimated Marginal Means drop-down menu, move Task Type to the Marginal Means box and select both Marginal means plots and tables.

Steps 4-8 should appear as follows:

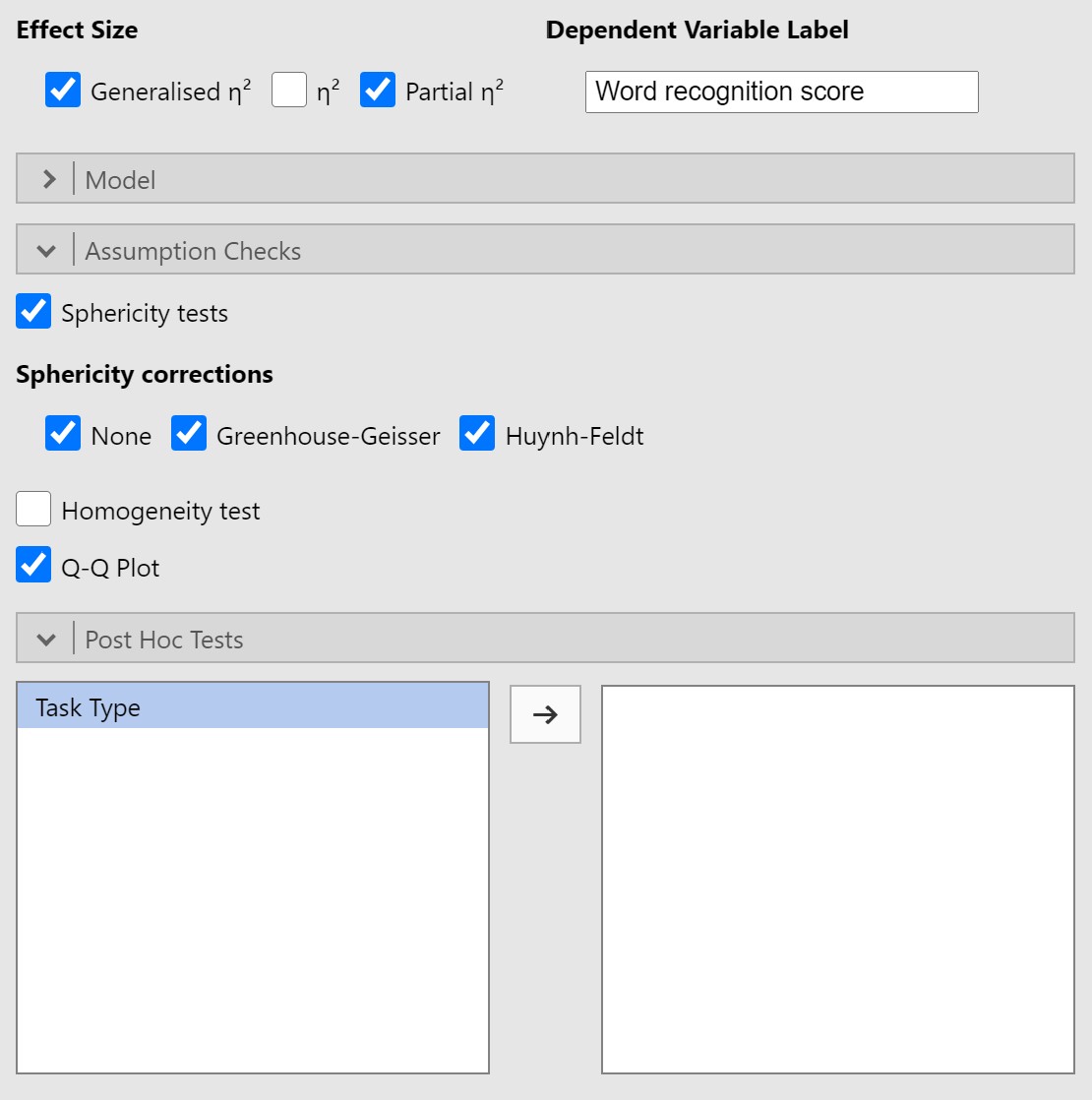
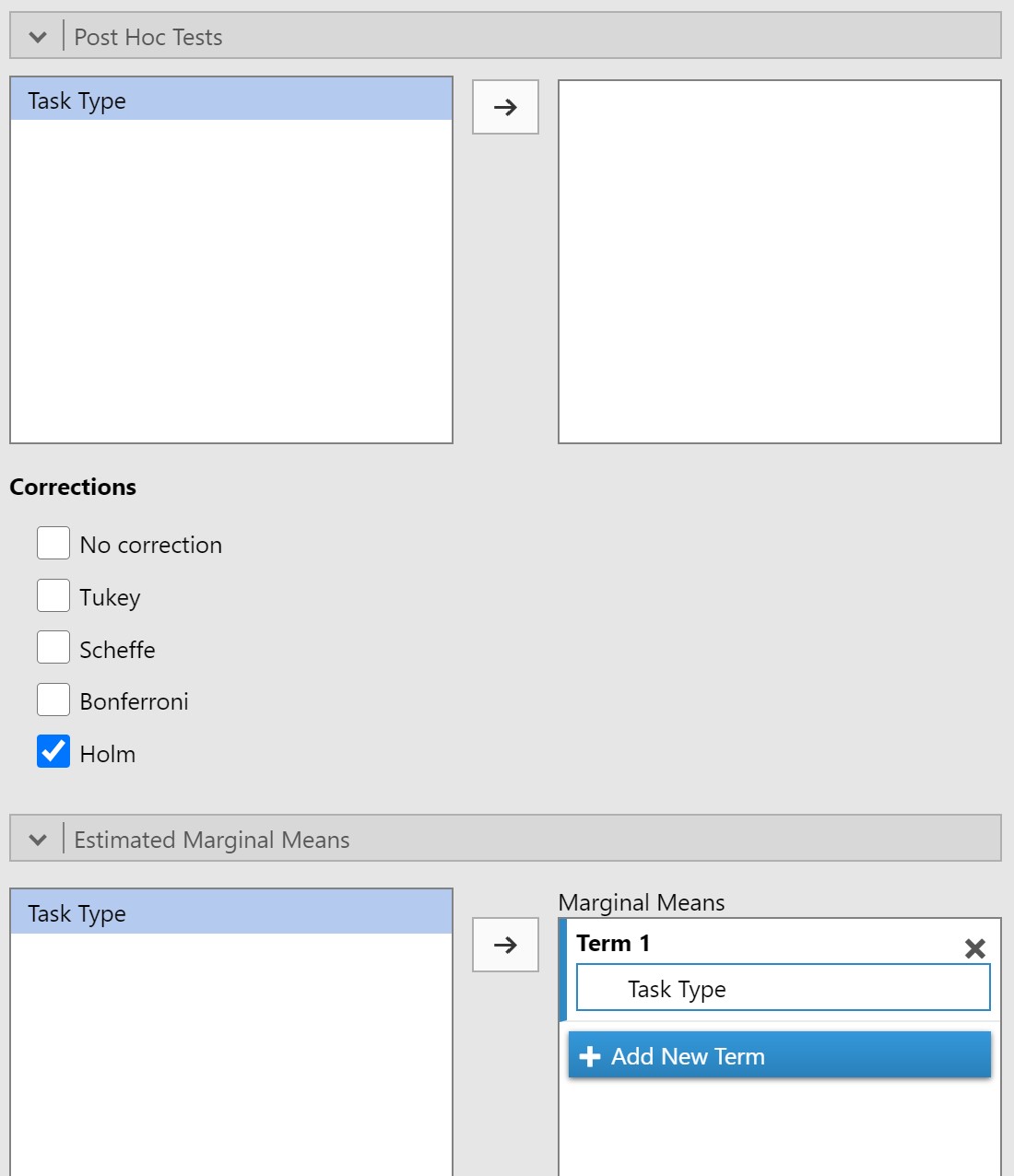
Note: you will notice that jamovi does not give us an option to run contrasts for repeated measures ANOVAs. Therefore, if you would like to run planned comparisons (based on a priori predictions about which specific level means will differ), then I recommend you follow the instructions under “What if jamovi does not have the contrast I want?” in the Follow-up tests section of Chapter 6.

4. Interpret Results

Let’s take a look at the results. The first part of the output will look like this:

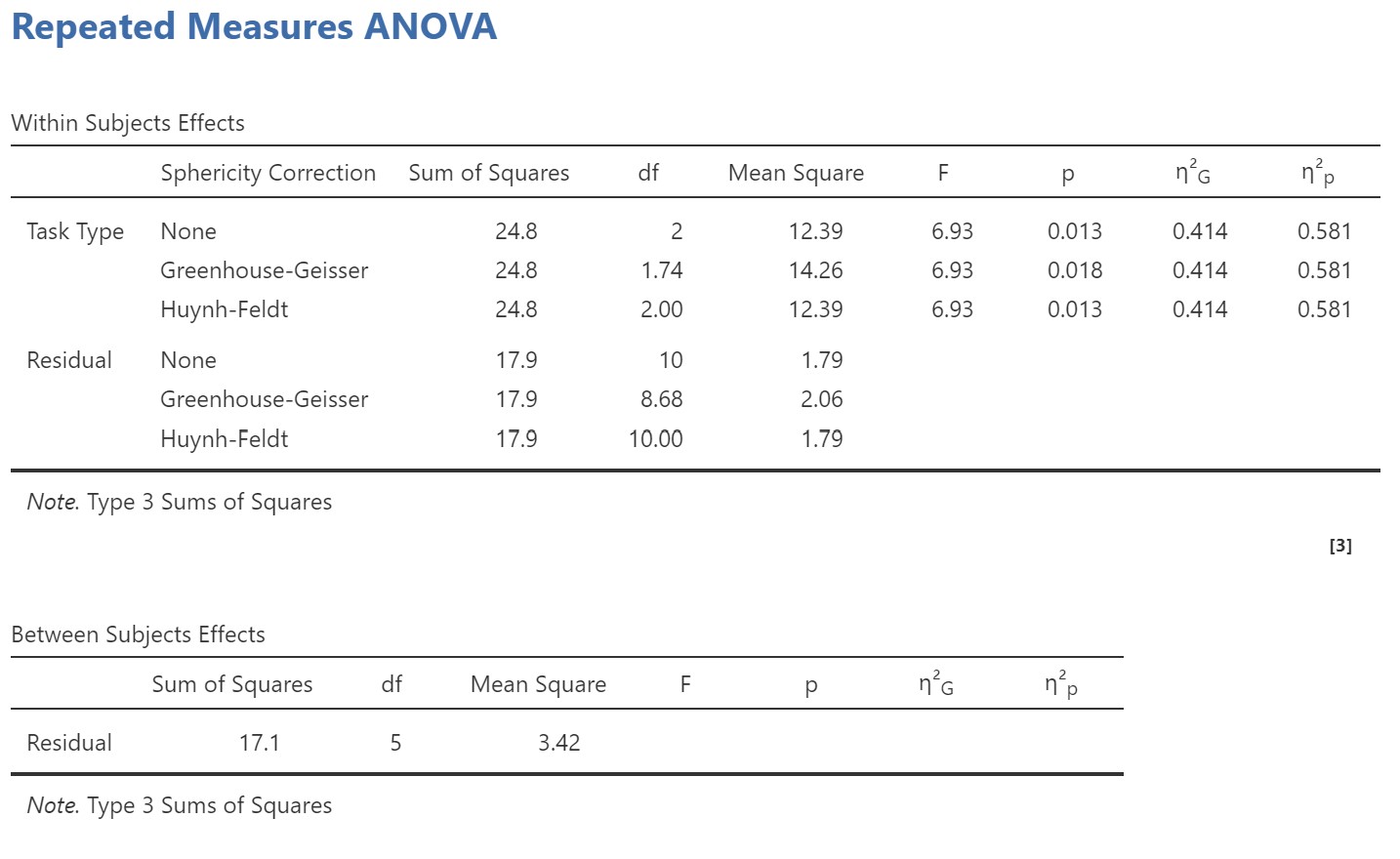
You’ll notice that jamovi provides you both a Within Subjects Effects table and Between Subjects Effects table. However, we only have a within-subjects effect (Task Type). With the repeated-measures ANOVA (which only has within-subjects IVs), we do not have any between-subjects independent variables so there is nothing to compute. We can ignore it in this case. It will be useful when we conduct a mixed factorial ANOVA, with both between-subjects and within-subjects effects (see later chapter mixed ANOVA).

Therefore, the Within Subjects Effects table is what we look at. Note that there are three rows for the effect of Task Type. This is because we requested no sphericity correction as well as both the Greenhouse-Geisser and Huynh-Feldt corrections. We can see that the df, MS, and p-value changes according to which correction we apply. The p-value is largest for the Greenhouse-Geisser correction, because this is the most conservative test. As mentioned in the previous section, I recommend using the Greenhouse-Geisser by default. We can see that the overall effect of Task Type is statistically significant (p = .018). Therefore we can look at our post hoc tests.

Another thing you may notice is that I asked for η²_p (partial eta-squared) as well as η²_G (generalised eta-squared). The η²_G value is slightly smaller and is actually the preferred measure of effects size for repeated measures designs (Bakeman, 2005).

Let’s look at the post hoc test results.

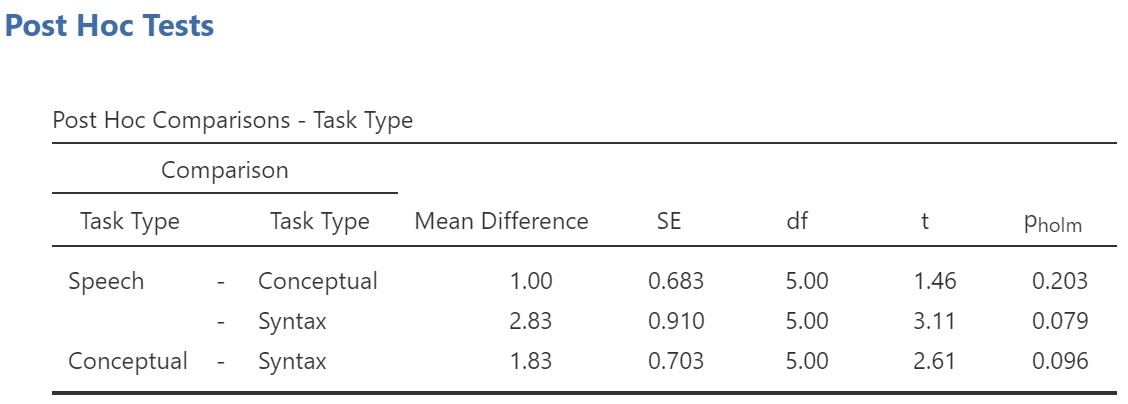
The Holm post hoc tests show that there were no significant differences among any of the means. How can this be, when the ANOVA was significant? Did we make an error in our analysis? We did not make an error in the analysis. This can happen, because ANOVA and post hoc tests are different tests. ANOVA is looking at how, overall, the level means vary around the grand mean in the experiment, whereas post hoc tests are making comparisons between pairs of means. It might be, for example, that if we collapse across two levels and compare them to the third level, there would be a significant difference, but we cannot conduct this analysis with post hoc tests. Remember as well that Holm corrects for the inflation of the family-wise error rate and so is somewhat conservative (if you run the post hoc tests again with no correction, you’ll see that two of the three comparisons are significant). Unfortunately, in this scenario, we may not have sufficient power (remember small sample size!) to detect where the differences between conditions lie.

Last, we can look at the Estimated Marginal Means – Task Type table to see the group means for reporting purposes.

Write Up the Results in APA Style

We can write this up in APA style similar to the one-way ANOVA.

A repeated measures ANOVA was performed examining how three tasks affected word recognition in patients suffering from Broca’s Aphasia. Task type significantly affected word recall (applying the Greenhouse-Geisser correction), F (1.74, 8.68) = 6.93, p = .018, η²_G = .41. Post hoc tests, applying the Holm correction, indicated no significant difference between any of the pairs of level means (speech task: M = 7.17, SE = .60; syntax task: M = 4.33, SE = .67; and conceptual task: M = 6.17, SE = .60), all p_holm > .05.

This is an interesting situation where the ANOVA gives a significant effect, but the post hoc tests are not significant. This can happen and is not too surprising in this case because the sample size is very small. Given the small sample size , it would have been advisable to conduct a non-parametric test. Let’s do that next.