The ${\mathrm{{\rm X}2}}^{}$ (chi-square) test of independence (or association) tests whether an observed frequency distribution of a nominal variable matches an expected frequency distribution, but unlike the goodness of fit test we are looking at the relationship, independence, or association between two variables. The test of independent tests whether two categorical variables are related or independent.

Our basic hypotheses for the chi-square test of independence is as follows:

• Null hypothesis: the observed frequencies match the expected frequencies. In other words, there are no differences in frequencies of how the levels in one variable relate to the levels in another variable.
• Alternate hypothesis: At least one observed frequency doesn’t match the expected frequency. In other words, at least one level has significantly different frequencies in another variable than we would expect.

1. Look at the Data

Let’s run an example with data from lsj-data. Open data from your Data Library in “lsj-data.” Select and open “chapek9.” This dataset indicates the ID number of the participant, the species (robot or human), and their preference of the three things (puppy, flower, or data).

For this example, imagine we are watching a show about the planet Chapek 9. On this planet, for someone to gain access to their capital city they must prove they’re a robot, not a human. In order to determine whether or not a visitor is human, the planetary beings ask whether the visitor prefers puppies, flowers, or large, properly formatted data files.

Data Set-Up

Our data set-up for a chi-square test of independence is pretty simple, We just need two columns of nominal data, with one row per participant, as we have in the chapek9 example (one column for species and one colour for choice).

Describe the Data

Once we confirm our data is setup correctly in jamovi, we should look at our data using descriptive statistics and graphs. Remember that for nominal variables we should report frequency statistics, not means and medians and such. Bar plots are also a good way of visualizing the data.

Specify the Hypotheses

The question here is whether humans and robots differ in preferring puppies, flowers, or data so we can determine who is a robot so only robots are let into the city. Therefore, our alternate hypothesis might be something like this: humans and robots have different preferences, or there is an association between species (human or robot) and preference (flowers, data, or puppies).

2. Check Assumptions

1. Expected frequencies are sufficiently large, which is usually greater than 5. If we violate this assumption, you can use Fisher’s exact test. We test for this assumption by selected “Expected counts” in the Cells tab for the test of independence. You will then see rows of expected counts in your contingency table. Look at the numbers and check that they are all 5 or greater.
2. Data are independent of one another, meaning each case contributes to only one cell of the table. If you violate this assumption, you may be able to use the McNemar test. This requires knowing how your data was collected. If it’s a within-subjects design with nominal variables, then most likely you want to use McNemar’s test. If it’s a between-subjects design that should be answered using a chi-square, then you most likely meet this assumption and can perform the chi-square test of independence.

3. Perform the Test

1. Go to the Analyses tab, click the Frequencies button, and choose “Independent Samples – ${\mathrm{{\rm X}2}}^{}$ test of association.”
2. Move your two variables into the rows and columns boxes. In this case, move choice into rows and species into columns. Note that the placement in rows or columns doesn’t really matter, but because we typically work with portrait pages I tend to prefer putting in rows whatever variable has more levels. In this case, choice has 3 levels and species only 2 so I like to put choice in rows and species in columns.
3. Under the Statistics tab, select ${\mathrm{{\rm X}2}}^{}$ under Tests and Phi and Cramer’s V under Nominal to get your effect size.
4. Select Expected counts under Cells to test your assumption of expected frequencies. Optionally, you can request the row, column, and total percentages. I often find these easier to report and interpret.
5. Select Bar Plot under plots. You may want to tinker with the settings here: in our case, I recommend using Side by side for Bar Type, and Rows for X-axis (that will put the choice on the x-axis, and I usually like to put the variable with the most levels on the X-axis for ease of interpretation). You can see if you prefer counts or percentages.

Ordinal Variable(s)

If either of your variables are ordinal, instead of selecting Phi and Cramer’s V, you should use Gamma or Kendall’s tau-b. Kendall’s tau-b should only be chosen if you have a square table (e.g., 3×3, 4×4, 5×5, etc.) whereas Gamma can be used with any size table. Kendall’s tau-b is also a slightly more conservative estimate compared to Gamma.

4. Interpret Results

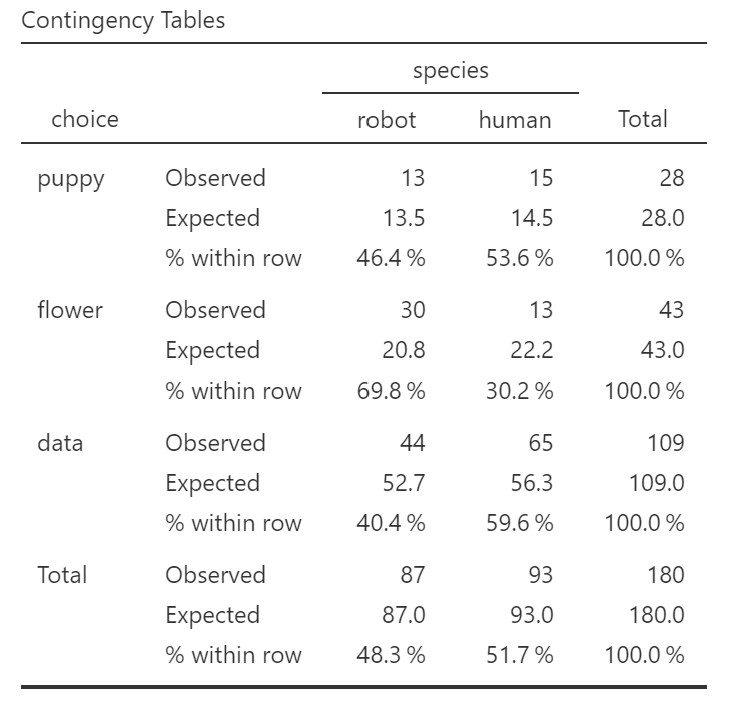
The first table shows us our observed and expected frequencies. We use the expected frequencies to test our assumption that expected frequencies are greater than 5. Our smallest expected frequency is 13.53 so we meet this assumption.

The second table gives us our results. Our p-value (p = .005) is less than .05 so we can reject the null hypothesis that the observed frequencies match our expected frequencies.

jamovi also gives us our Cramer’s V value. Note that it does not provide Phi because we don’t have a perfect square table (e.g., 2×2 or 3×3). These are measures of effect size for the chi-square. Cramer’s V can be interpreted similar to a correlation (ranges from 0 to 1, with higher scores meaning stronger relationships between the variables).

Write Up the Results in APA Style

We can write up our results in APA something like this:

The ${\mathrm{{\rm X}2}}^{}$ test of independence showed a significant association between species and choice, ${\mathrm{{\rm X}2}}^{}$(2) = 10.72, p = .005, Cramer’s V = .24. Robots, compared to humans, were more likely to say they prefer flowers (robots: 70%; humans: 30%) and humans, compared to robots, were more likely to say they prefer data (humans: 60%; robots: 40%). Robots (46%) and humans (54%) were equally likely to prefer puppies.

Visualize the Results

Here’s the plot I was able to produce in jamovi. Note that there are multiple ways to present the plots, so think about which way will best support the results.

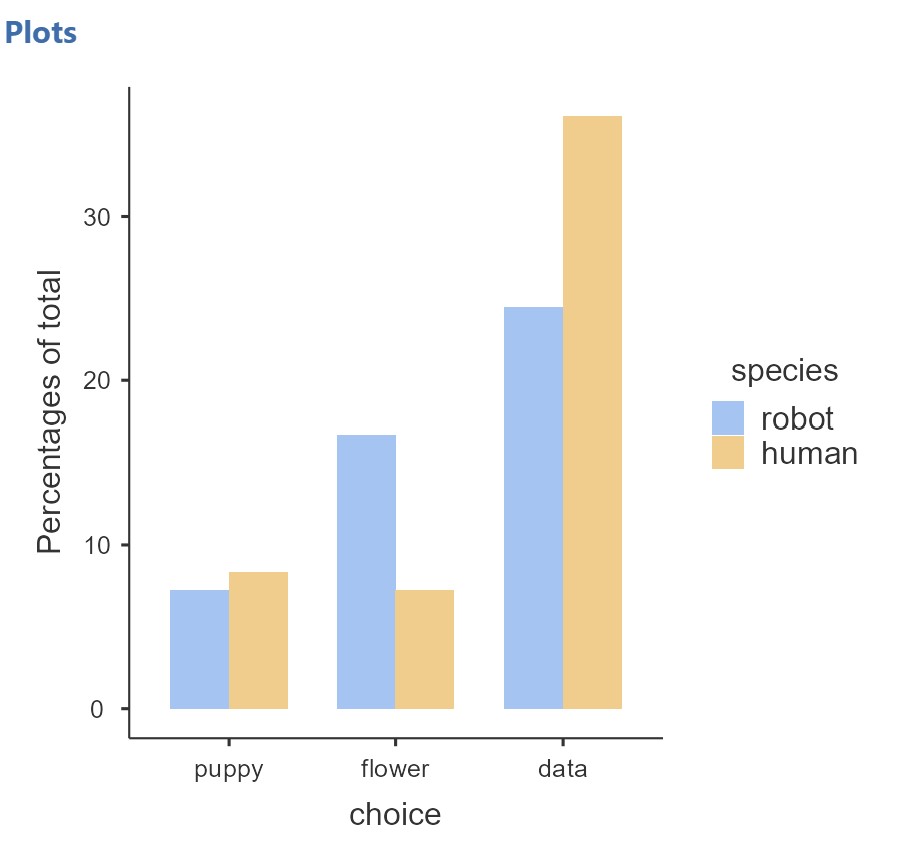
Unfortunately, jamovi does not have any options for changing the colour of the bars or for editing any other details of the plots (e.g., axis labels, legend, etc.). The jamovi plots are fine for this class, but if you are working on a thesis, a poster for presentation at a conference, or a an manuscript for publication, it would be best to use Excel (or some other software for creating your plots).

Fisher’s Exact Test

If you violate the assumption that there your expected frequencies are sufficiently large and you have a 2×2 table, you can still perform the test of independence but instead of selecting ${\mathrm{{\rm X}2}}^{}$ you’ll select Fisher’s exact test. You’ll interpret your results in exactly the same way, but specify that you used Fisher’s exact test.