44 Chi-Square Goodness of Fit
The Χ2 (chi-square) goodness of fit tests whether an observed frequency distribution of a nominal variable matches an expected frequency distribution. Our hypotheses for the test are as follows:
- Null hypothesis: The observed frequencies match the expected frequencies. In other words, the frequencies of the variable are what we would expect.
- Alternate hypothesis: At least one observed frequency doesn’t match the expected frequency. In other words, the frequencies of at least one level of the variable are not what we would expect.
Note that these are not how you should describe your hypotheses! You should specify your hypotheses in relation to the nature of your data. For example, if we have a deck of cards and want to see if people don’t choose cards randomly, the null hypothesis would be that there is a 25% probability of getting each hearts, clubs, spades, and diamonds.
1. Look at the Data
Let’s run an example with data from lsj-data. Open data from your Data Library in “lsj-data.” Select and open “randomness.” This dataset has participants pull two cards from a deck. For now, we’re just going to work with choice_1. We’re interested in finding out if participants pull cards randomly from the deck.
Data Set-Up
Our data set-up for a chi-square goodness-of-fit test is pretty simple, We just need a single column with the nominal category that each participant is in. In the example, the nominal category we are going to work with is choice_1 (which suit the participant chose).
Describe Your Data
Once we confirm our data is setup correctly in jamovi, we should look at our data using descriptive statistics and graphs. First, our descriptive statistics are shown below. With nominal variables like choice_1, we should request Frequency tables, not descriptive statistics like the mean and median. The mean for choice_1 would be, quite frankly, meaningless. What’s the average card type? It can’t exist. So we do frequencies instead. Under Plots we can select a Bar plot to visualize the data appropriately.
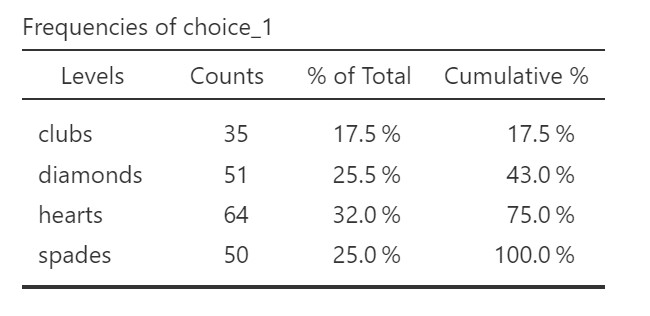
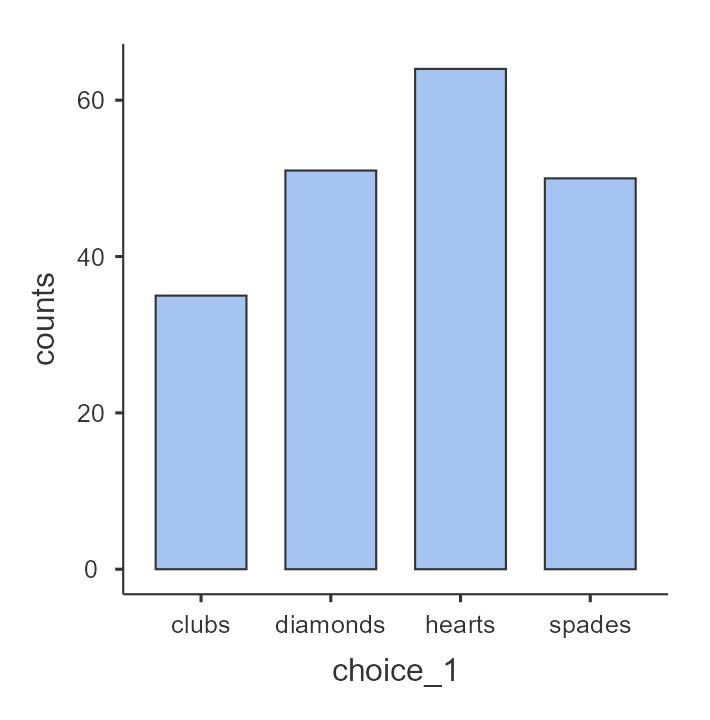
Notice how jamovi is pretty smart here and knows not to give us the mean, median, minimum, and maximum. Check the box for Frequency tables to receive those. From our data, we see that most participants pulled a hearts card first (n = 64, 32%) followed by diamonds (n = 51, 26%), spades (n = 50, 25%), and finally clubs (n = 35, 18%).
Specify the Hypotheses
We’re interested in finding out if participants pull cards randomly from a deck of cards. A typical deck of cards has 52 cards, 13 for each of the four suites (clubs, spades, hearts, diamonds). Because there are 4 suites, then 1/4 is 25% which is our expected frequency of pulling cards randomly from the deck. Under the null hypothesis, we expect that participants pull cards randomly from the deck. In other words, there is a 25% probability of pulling each of hearts, clubs, spades, and diamonds. Under the alternate hypothesis, we expect that participants pull cards not at random from the deck. In other words, participants have a probability other than 25% of pulling at least one of the types of cards.
2. Check Assumptions
The chi-square goodness-of-fit test has just one assumption: Expected frequencies are sufficiently large, which is usually greater than 5.
You test for this assumption by checking the “Expected counts” box (see 3. Perform the test, below). You will then see rows of expected counts in your contingency table. Look at the “expected” numbers and check that they are all 5 or greater.
3. Perform the Test
To perform the chi-square goodness of fit test, do the following steps:
- Go to the Analyses tab, click the Frequencies button, and choose “One sample proportion tests – N outcomes.”
- Move your variable into the Variable box. In this case, move choice_1 into the Variable box.
- Select Expected counts so you can check for your assumption of expected frequencies.
When you are done, your setup should look like this:
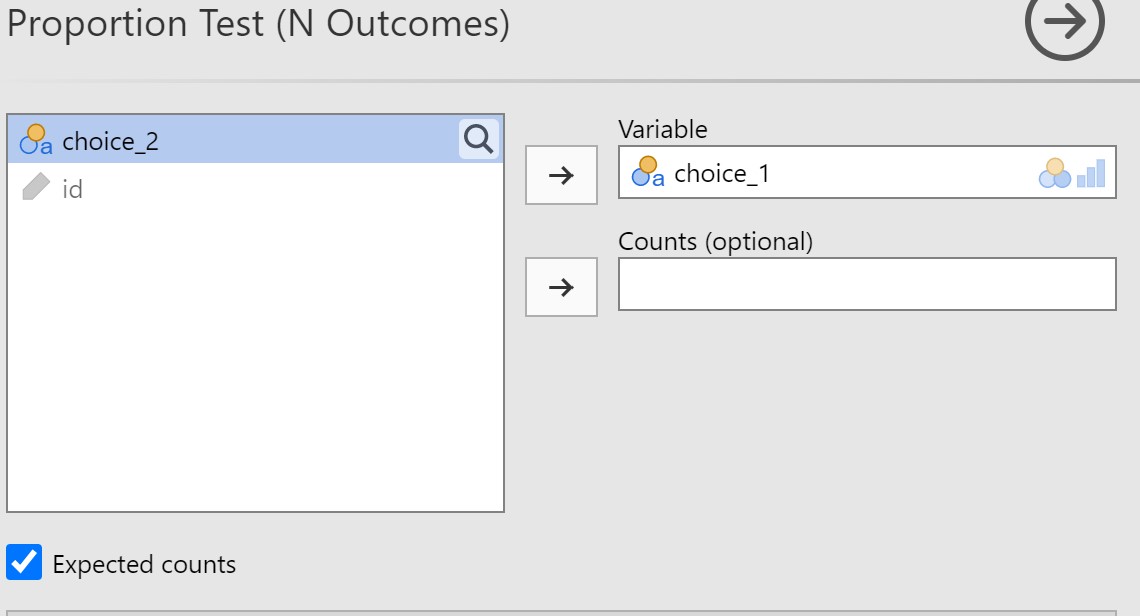
As you will see in the output, jamovi automatically assumed equal proportions of frequencies (in this case 1/4 or 25% chance of pulling each card). However, there might be times when you don’t want to make that assumption. Maybe we’re testing the whether our sample frequencies match the population frequencies and those are uneven (e.g., whether our 80/20 right/left-handedness split in our sample matches the 90/10 handedness split in the population).
We can use the Expected Proportions in the setup to specify different expected frequencies.
4. Interpret Results
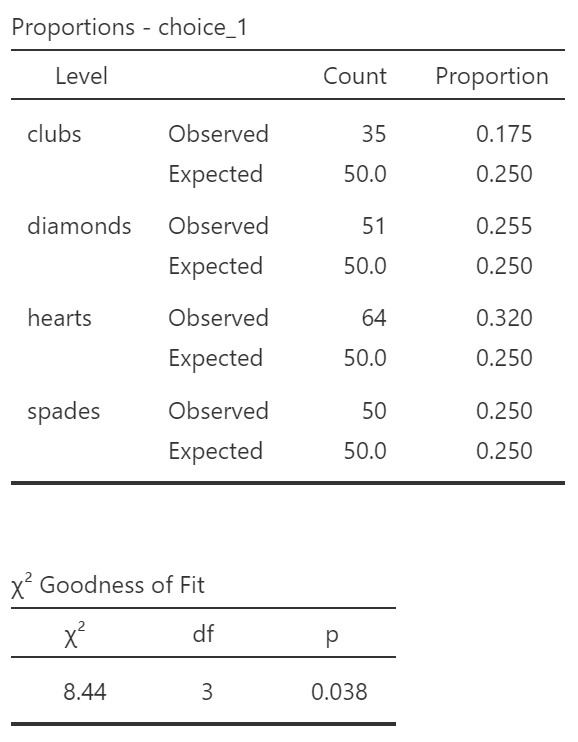
The first table shows us our observed frequencies (our data) and expected frequencies (N/k = 200/4 = 50 which is 25% for each one, like we previously calculated).
The second table gives us our results. Our p-value is less than our alpha of .05 so we can reject the null hypothesis that the observed frequencies match our expected frequencies.
Write Up the Results in APA Style
We can write up our results in APA something like this:
Of the 200 participants in the experiment, 64 selected hearts for their first choice, 51 selected diamonds, 50 selected spades, and 35 selected clubs. A chi-square goodness of fit test was conducted to test whether the choice probabilities were identical for all four suits. The results were statistically significant, Χ2(3) = 8.44; p = .038, suggesting that people did not select suits purely at random. Participants chose the hearts (32%) more frequently than expected and the clubs (17%) less frequently than expected.
Note that I described the data in the first sentence, but I could have also described it in more detail in the last sentence as part of my interpretation or I could have even written up the results in a table!
