When people talk about doing power analysis, really what they should be saying, usually, is sample size determination.

Here are a few key points to get you started.

1. When designing your research, aim for a large effect, small variability, and as large a sample as is necessary to achieve desired power (80% or more).
2. Before you start to collect data, you should decide what sample size is necessary to achieve desired power (i.e., an a priori power analysis or sample size determination). To determine what sample size is necessary, based on an expected given effect size and variability, use software like G*Power (it is free, and moderately complicated to use, depending on what you are trying to achieve). Fortunately, jamovi will also allow you to do some simple sample size estimation in the jpower module.
3. Always report confidence intervals and effect sizes, not just p-values! We shall look at appropriate measures of effect size for each of the tests we use in this course. Fortunately, jamovi will typically compute these for you.

When it comes to sample size determination, sometimes, for various reasons, you cannot obtain the desired sample size. For example, you might only have two weeks to collect data for a class project or your population of interest is difficult to recruit or test (e.g., babies or people with a specific medical condition). Therefore, when we think about power and sample size determination, there are three things you might be interested in figuring out:

1. What sample size do I need given the effect size of interest, alpha level, and power level?
2. What power do I have to detect the effect size of interest given my alpha level and sample size?
3. What effect size can I reasonably detect given my alpha level, power level, and sample size?

Sample Size Determination

Let’s say we want to address the first of the three above: for a specified level of power, alpha, and given effect size of interest, we are going to determine what sample size we need.

Note that the jpower module in jamovi is fairly limited in the analyses you can do. (You can install jpower by clicking on the at the top right hand corner of the screen in jamovi. Then select jamovi library, scroll down to find jpower, and install it.) If you need to determine sample sizes for other types of analyses, then go to G*Power or, better yet, ask someone with experience in R to do it for you in R.

jpower will allow you to compute the required sample size for t-tests, only. To do this, open a blank jamovi datafile (click on the hamburger in the top left corner, and select New). Click on the jpower module and choose the kind of test you plan to run in your study (as I mentioned, this is limited to t-tests).

Let’s say we are going to have a two-group between-subjects design, for which we shall run an independent samples t-test. We want to know how many participants we shall need in each group in our study. You will need to decide a few things. A minimum level of acceptable power is typically set at 0.8 (80%), but you can also run the analysis for different levels of power. I would plan to have the same number of participants in each group (though you can specify a different ratio if you need to, by changing the Relative size of group 2 to group 1) and assume for this demonstration that you are confident about being able to run a one-tailed test (you have a clear, directional hypothesis, based on prior research and/or theory: e.g., you expect group A to score higher than group B, and not the other way around). You can use α = .05.

Finally, you need to choose the minimally-interesting effect size. According to Daniel Lakens (https://psyarxiv.com/9d3yf/), there are a few ways to decide on what effect size interests you:

1. “Smallest effect size of interest: what is the smallest effect size that is theoretically and practically interesting?
2. Minimally statistically detectable effect: given the test and sample size, what is the critical effect size that can be statistically significant?
3. Expected effect size: which effect size is expected based on theoretical predictions or previous research?
4. Width of confidence interval: which effect sizes are excluded based on the expected width of the confidence interval around the effect size?
5. Sensitivity power analysis: across a range of possible effect sizes, which effects does a design have sufficient power to detect when performing a hypothesis test?
6. Distribution of effect sizes in a research area: what is the empirical range of effect sizes in a specific research are, and which effects are a priori unlikely to be observed?” (p. 3)

Basically, these are saying: what does past research have to say about what effect size you can expect (#3 and #6)? What is the smallest effect size you care about (#1)? Consider how important it is to spend time/money/other resources chasing small effect sizes. If your research could have profound consequences for society even with really small effect sizes, then it might be worth it. In other situations, you might decide that it is only worth looking for a medium effect size. What is the smallest effect size you can reasonably obtain (e.g., due to sample size limitations; #2, #3, and #4)? This is the justification you use to determine what effect size you are looking for. Note that in jamovi, the δ (Greek delta symbol) denotes Cohen’s d.

Let’s say you decide that it is reasonable to expect/look for a medium effect size of d = 0.5, aiming for power = 80%. This is what you should see in jamovi:

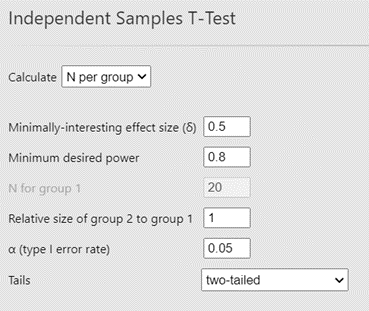
To the right, jamovi automatically populates the “Results” pane. You will see that you will need 64 participants in each of your two groups to achieve 80% power with effect size d = 0.50

You can also select different plots. Check all the boxes and also ensure you check the box next to Explanatory text, under Additional Options. jamovi provides a very detailed explanation of what each plot shows you.

The Power Contour graph shows you the relation between power, effect size and sample size. From this you can get a sense of how much power you will have if your effect size turns out to be smaller or larger or if you do not reach your intended sample size.

The Power Curve by N graph gives you a sense of how much you would need to increase your sample size if you wanted to achieve 90% power (somewhere closer to 100 per group). You might want re-run the test with power set to 0.9 and see what happens…. Now you will need 86 per group.

What to aim for? Well, of course 90% power is better than 80% power, but if you have limitations on your data collection (e.g., the pool of participants is not that large), you might just aim for 80% power.