6 Inferential Statistics 101
There are some fundamental principles that all the test statistics (t, r, F, etc.) draw on. Let’s go back to Max’s research question from the first chapter: Do redheads appear more friendly than other people? If we had infinite capacity for testing participants, we could gather up all the people in the world and present them all with photos of redheads and people with other coloured hair and ask them to rate the friendliness of each photo. Of course, we cannot do this, so we just test a sample of participants from the population and use those data to make inferences about the population. Hence, we use inferential statistics, to infer the characteristics of the population from our sample.
Null Hypothesis Significance Testing
How do we do that? We are going to use null hypothesis significance testing (NHST). First, Max sets up his null and alternative hypotheses. Assuming there is some prior research and theory to support Max’s idea, we might suggest:
Alternative hypothesis (H1): Participants will rate redheads as more friendly than non-readheads.
Null hypothesis (H0): There will be no difference in ratings of friendliness for redheads and non-redheadeads OR participants will rate redheads as less friendly than non-readheads.
Note that I have set this up as one-tailed or directional hypotheses. If I had two-tailed or non-directional hypotheses, what might they be?[1] (Note that, either way, I have to ensure that all possible results are captured.)
Now, Max goes out and collects some data with 30 participants (N = 30) and finds that the participants do indeed rate the redheads as more friendly than the non-redheads. However, it’s important to realize that the difference in ratings in our sample is unlikely to be exactly zero, even if the null is true. What we need to find out is how big the difference in ratings should be for us to reject the null hypothesis. How do we do that?
From Sampling Distributions to p-Values
First, we generate a sampling distribution: for this, we start by assuming that the null hypothesis is true, and that there is no difference between the friendliness ratings for redheads and nonredheads (mean difference = 0). We imagine going into the population an infinite number of times, collecting an infinite number of random samples the same size as our sample (N = 30 in this case), calculating the mean difference for each sample, and plotting the frequency of those means differences. We might get something like this:
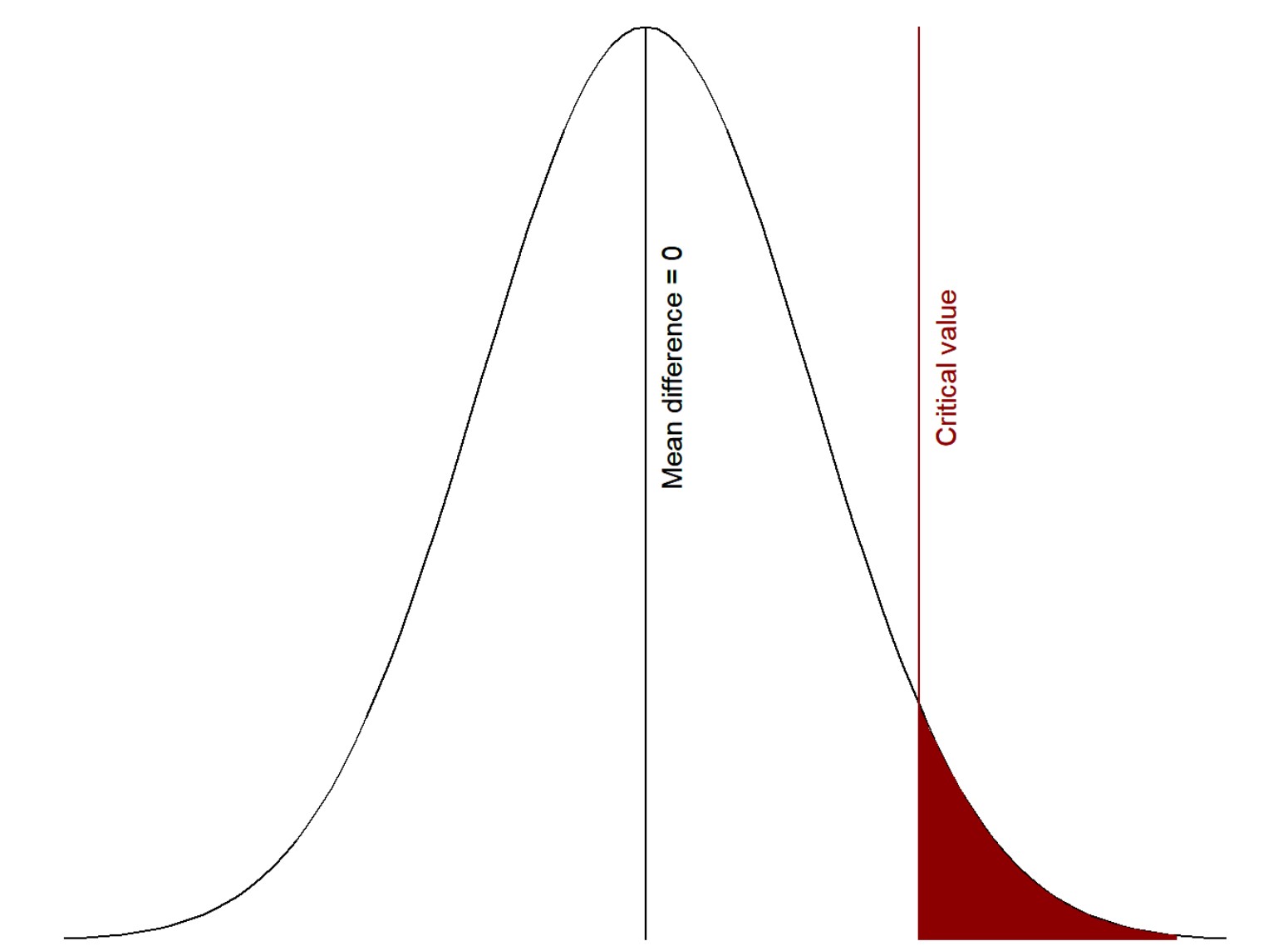
As you can see from the figure, we would get many samples where the mean difference = 0 (high frequency), quite a few samples where the mean difference is a bit above or below 0, and far fewer samples where the mean difference is much larger or smaller than 0.
Next, we decide on our critical value, shown on the figure as a red line. This is determined by our alpha level, which we have set as our level of significance. Most studies you read use the arbitrary = .05 (5%). In the visualization above, we set the alpha to 5% and so the area shaded in red is exactly 5% of the area under the curve of the normal distribution.
Our critical value is the level at which we are saying we would consider it “surprising” (versus “not surprising”) if we got a mean difference that large or larger (i.e., the red region in the graph) assuming that the null hypothesis is true. Basically, if we assume there truly is a mean difference of 0 in the population (i.e., the null hypothesis), values beyond the critical value would be considered surprising enough that we would say that we reject the null hypothesis. This is why it is called null hypothesis significance testing.
In other words, the area in red are values that are unlikely to occur if the null hypothesis (in this case, mean difference <= 0) were true. In fact, we would get a mean difference in the red region 5% of the time, in the long run, if the null hypothesis were true.
A bit more about sampling distributions
There are many different kinds of sampling distributions. Every statistic that we use has sampling distributions associated with it: there are sampling distributions for t, r, F, and so on, and in each case they vary in shape according to the degrees of freedom.
Also, you should be aware that we do not actually go out and create the sampling distribution. It is a theoretical distribution. In addition, we do not have to calculate the critical value ourselves, thanks to the work of some fancy mathematicians in the days before computers! Based on the incredible properties of the normal distribution, they figured out what the sampling distributions of all the test statistics we need to use would look like. They determined how the shape of those distributions would change according to sample size (or, to be more precise, degrees of freedom). And they calculated the critical values for each test statistic depending on the direction of the hypothesis and alpha level. In your lower level stats class, you probably looked these things up in a table in a book, but in this class, our statistical software will generate the information we need.
When you run your inferential statistics using statistical software (jamovi, SPSS, or whatever software you plan to use), you will obtain the actual value for the test statistic in your sample and a p-value. This p-value represents the probability or the likelihood of getting that value for the test statistic or more extreme, in the long run, when the null hypothesis is true. If p < .05, we figure we are pretty unlikely to get a value that extreme or more extreme when the null is true, and so we reject the null hypothesis.
So to sum up:
- We generate a sampling distribution for our test statistic;
- We calculate the test statistic for our particular sample; and
- We find out how likely we are to get that value or a more extreme value for that test statistic, when the null hypothesis is true, in the long run, i.e., the p-value.
Type 1 and Type 2 errors
There is one more thing to keep in mind: we can be wrong! Just because we get a result does not automatically mean that result is 100% accurate. There are many things that could lead us to an inaccurate interpretation!
We can use the table below when discussing errors. On the far left column, we have our results: were they statistically significant (p < .05) or not (p > .05)? On the top row, we have whether in the real world the null or alternative hypothesis is true. In reality, we can never truly know whether the null or alternative hypothesis is true. We can at best approximate our understanding of the real world through replication!
| H0 is true | H1 is true | |
| p < .05 (statistically significant) | Type 1 error (alpha) | Correct interpretation |
| p > .05 (statistically non-significant) | Correct interpretation | Type 2 error (beta) |
Therefore, any time we get a statistically significant result (p < .05), then either we made a correct interpretation or we made a Type 1 error!
Similarly, any time we get a statistically non-significant result (p > .05) then either we made a correct interpretation or we made a Type 2 error!
What does a p-value tell you?
The p-value does not tell you:
- The importance of an effect
- When the null hypothesis is true
- When the null hypothesis is false
It does tell you: the probability (in the long run) of getting a test statistic this extreme, or more extreme, if the null hypothesis were true.
Confidence Intervals
Again, when we use inferential statistics, we are aiming to infer something about the population from our sample. In a very simple model, we can use our sample mean as an estimate of the population mean. This is called point estimation. However, it may not be very accurate. We might be better off estimating the population mean by giving a range of values within which the population mean might fall. To do this, we use confidence intervals (interval estimation). Confidence intervals (CIs) are a statistical way of saying “around.” Specifically, a 95% CI for a mean tells us that 95% of the time, in the long run, the CI will contain the true value of the population mean. We can compute confidence intervals around not just means, but also around our statistical test values (e.g., t, r, etc.) and around effect sizes.
Parametric and Non-Parametric Tests
As you learn more about statistics (and later in this book) you will notice that there is a distinction between parametric and non-parametric tests. These are both kinds of inferential statistics. However, parametric tests make certain assumptions about the data (e.g., that the variances for different groups in the experiment should be homogenous) and so we cannot use them in all situations. On the other hand, non-parametric tests make fewer assumptions and so can be useful when our data violate the assumptions of a parametric test. More about assumptions and the non-parametric alternatives to parametric tests as we proceed through the books.
Choosing the Correct Statistical Test
It is important that you learn how to identify which inferential statistic you should perform. This chart can help you determine what statistical test to perform. Note that on the right dark red boxes are parametric tests, light red boxes are non-parametric tests, and white boxes will not be covered in this class at all (in fact, there are many others not even shown that we won’t cover!). Data types are indicated in either blue (continuous), green (categorical), or teal (both). Number of variables or levels of the variables are either 1 (light orange), 2/2+ (orange), or 3+ (dark orange). Between-subjects designs, meaning designs with different participants in each group, are in black whereas within-subjects designs, meaning designs with the same participants in each group, are in light grey.
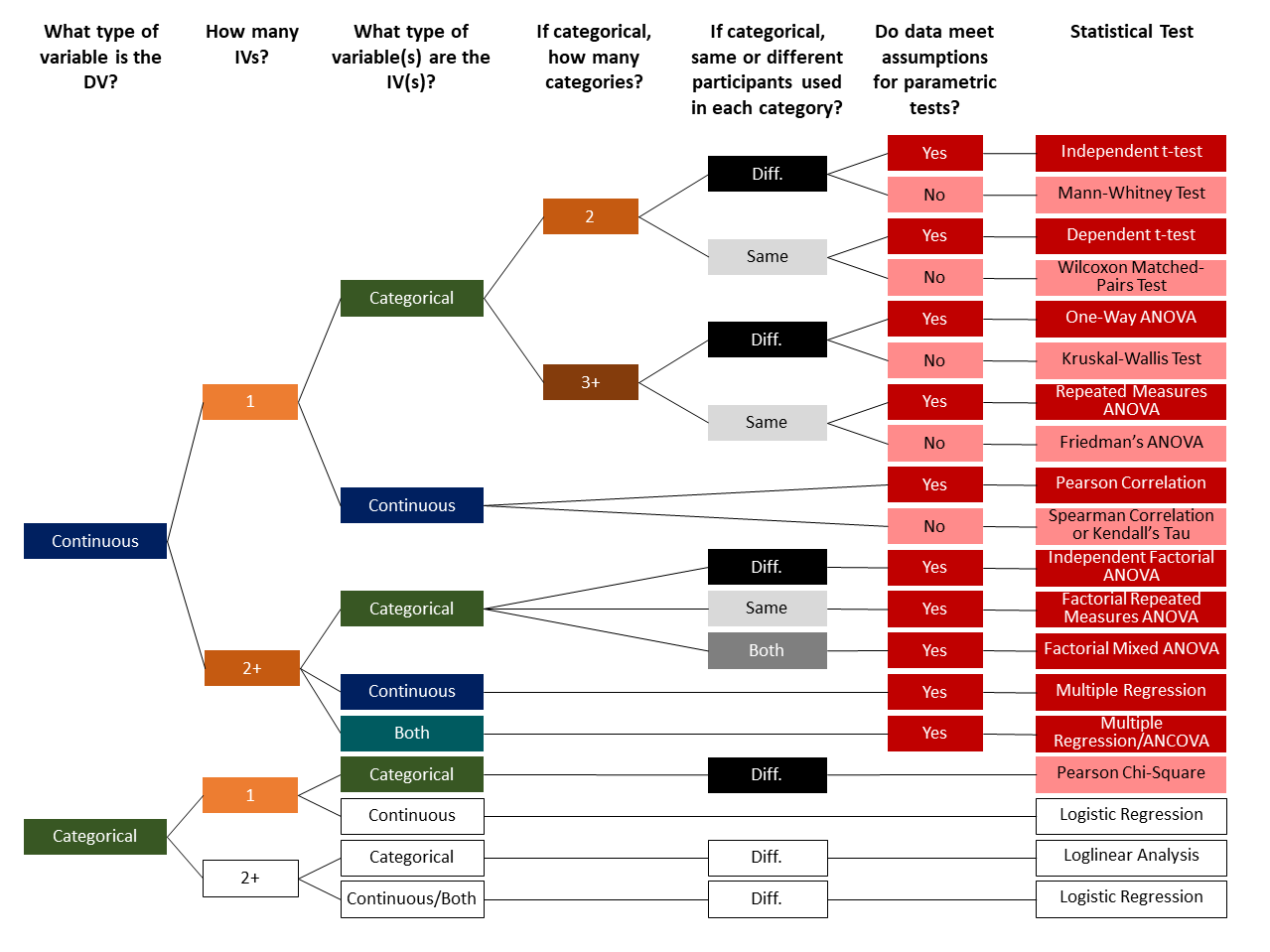
First, you need to determine what level of measurement your dependent variable (DV) is. We will only be covering statistical tests that have one dependent variable. Therefore, you need to know whether the variable is categorical (i.e., nominal or ordinal) or it’s continuous (i.e., interval or ratio).
Next, you need to determine how many independent variables (IVs) there are and then what level of measurement your IV(s) are. In the case of a single categorical IV, we also need to know how many levels there are to the IV (i.e., how many categories there are). For categorical variables, we also need to know if the participants are different (i.e., between-subjects) or the same (i.e., within-subjects) within each level of the category.
Lastly, for many of the statistical tests we need to know whether we meet the assumptions of parametric tests. If we don’t meet the assumption, then there are alternative tests we can perform.
We can both forward map and backwards map with the chart above. Forward mapping involves understanding your data and your research question and then determining what statistical test to perform. Forward mapping is mostly what you need to understand how to do! Backwards mapping involves determining what kind of data is needed to perform a particular statistical test. This is more for educational and understanding purposes and generally is not how you analyze data.
Forward Mapping: Choose the Correct Test
A researcher is interested in understanding whether athletes have higher English scores than non-athletes. In other words, what is the effect of athletic status on English test scores?
- What is the DV? What is the level of measurement? It’s English test scores, which is a continuous variable.
- How many IVs are there? We only have one IV, and it is athletic status.
- What is the level of measurement of the IV? Athletic status is a categorical variable.
- How many categories to the IV? Athletic status is measured as either athlete or non-athlete, so there are 2 levels.
- Are the same or different participants used in each category? People can either be an athlete or not an athlete, but they can’t be both, so this is a between-subjects variable (aka “different”).
- Do data meet the assumptions for parametric tests? We don’t know. We would need to test this. For now, let’s assume we meet the assumptions.
- Statistical test? Independent t-test
A researcher is interested to know whether people perform better on the exam at the start, middle, or end of the semester. The researchers has all participants complete all three exams.
- What is the DV? What is the level of measurement? In this case, the exam is our DV and it’s a continuous variable.
- How many IVs are there? We only have one IV, and it is time of the exam.
- What is the level of measurement of the IV? The time of the exam is a categorical variable.
- How many categories to the IV? Type of test has three categories: start, middle, or end of the semester.
- Are the same or different participants used in each category? Although the researcher could have designed a between-subjects design, this particular study has all participants participate in all conditions, so it is a within-subjects design (aka “same”).
- Do data meet the assumptions for parametric tests? We don’t know. We would need to test this. For now, let’s assume we meet the assumptions.
- Statistical test? One-way repeated measures ANOVA
- Alternative hypothesis: participants will rate redheads differently from non-redheads. Null hypothesis: there will be no difference in ratings of friendliness for redheads and non-redheads. ↵
