When we compute a Pearson correlation coefficient (the statistical test we shall learn more about shortly), we compute r. The value for r can range from -1 (perfect negative correlation) through 0 (no correlation) to +1 (perfect positive correlation). The larger the absolute value of the correlation coefficient, the stronger the relationship. When r is negative, as x (one variable) increases, y (the other variable) decreases. When r is positive, as x increases, y also increases. One thing to watch out for is that Pearson’s r will only tell us about the strength of a linear relationship.  That is, if we have a curvilinear relationship (e.g., U-shaped, inverted-U, or S-shaped), we might have a small value for r even though the relationship between x and y is actually strong! We shall have a look at some examples of this in class.

Let’s take a brief look at how to compute Pearson’s r and how to interpret it.

Computing r

Covariance

Correlation is computed by first calculating something called covariance, which indicates how much two variables vary together (i.e., covary). You may recall that variance tells us how much scores deviate from the mean for a single variable. Covariance is similar: it tells us by how much pairs of scores on two variables differ from their respective means. Covariance is calculated by the following formula:

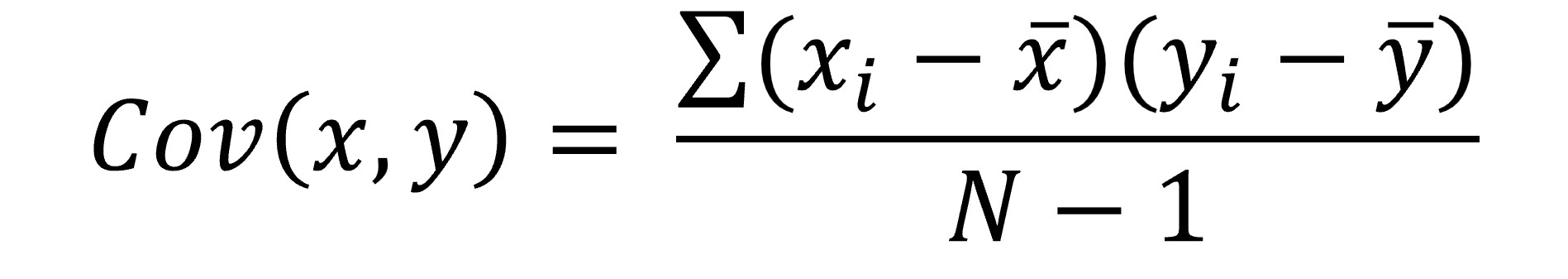
What this means is that to calculate the covariance of x and y, we compute the product of the difference between each x score (x_i) and the mean of x and each y score (y_i) and the mean of y, for all the pairs of x scores and y scores in our sample. We sum those products and divide by the degrees of freedom (N-1).

Therefore, if high scores on x are consistently paired with high scores on y, and low scores on x are consistently paired with low scores on y, the value for covariance will be large and positive. If high scores on x are consistently paired with low scores on y, and low scores on x are consistently paired with high scores on y, then the value for covariance will be large and negative. In contrast, if there is no relationship between x and y – sometimes high scores on x are paired with low scores on y and sometimes with high scores, and so on, then the products of the deviations will sometimes be positive, sometimes negative, and sometimes large, and sometimes small, and so when they are summed, the result will be close to zero, i.e., small covariance.

Pearson’s r

However, we cannot use covariance as a measure of the strength relationship between x and y, because the size of the standard deviations of x and y affect the value of covariance. Therefore, we scale covariance by the size of the standard deviation. Pearson’s correlation coefficient is computed as follows:

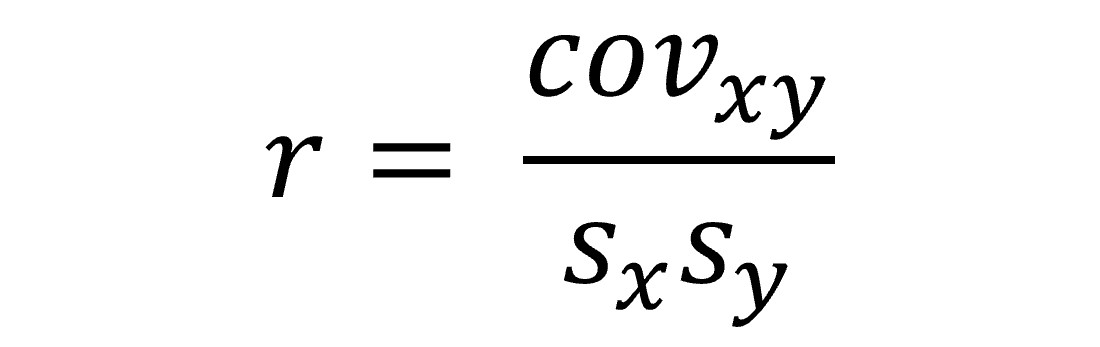
In the next chapter, we shall look at how to obtain the Pearson’s correlation coefficient in jamovi.

Interpretation of r

A rough guide to the interpretation of the value of r, when used to describe the strength of the association between two variables, is as follows:

• +/- .1 = weak relationship
• +/- .3 = moderate relationship
• +/- .5 = strong relationship

Note that these are just general guidelines and that we should also think about the strength of the relationship in practical terms and in relation to our area of study.

We can also compute r², the coefficient of determination, which indicates the proportion of the variance in one variable shared by the other variable. We shall learn more about this in the chapter on regression.

Using r

Pearson’s r can be used for a number of different purposes. Earlier in this chapter we have used the example of testing whether there is a relation between sleep quantity and morning grumpiness. In this case, we would use r to describe the strength and direction of the relation between our two variables – just to describe the results of the study.

In other situations, we may use r to look at a measure we have developed. In that case, we can use r to assess the reliability of the measure, including inter-rater reliability (the extent to which two different raters assign the consistent scores on the measure), test-retest reliability (the extent to which participants obtain the same score on a measure when re-tested), and split-half reliability (the extent to which participants’ scores on half of the items on the measure correlate with the scores on the other half of the items). When using r to assess the reliability of a measure, then researchers are typically looking for higher values than when using r to describe the results of the study. Reliability of r = 1.0 would be rarely (never) obtained, but coefficient of r = .80 or above are often considered to be very good. Further discussion of this issue is beyond the scope of this class.

We can also use r to assess the validity of a measure, including convergent validity (the extent to which scores obtained on one measure are correlated with scores on another similar, previously-validated, measure); discriminant validity (the extent to which scores obtained on one measure are not correlated with scores from a measure of a different construct); and criterion validity (the extent to which a measure correlates with either a current behaviour – concurrent validity, or a future behaviour – predictive validity).

Playtime: Getting a Feel For r

Want to learn a bit more about what different values of r look like in a dataset? Try going to www.guessthecorrelation.com to see how well you do in guessing the value of r for different datasets! Another great website to play around with data to see how it affects the value of r is here: https://rpsychologist.com/correlation/