33 Mixed ANOVAs
What is Mixed ANOVA?
When we have both between-subjects and within-subjects independent variables (at least one of each) we have what is called a mixed design. Imagine, for example, that students in Dr. Chico’s class (whose data we used in chapter 5 on t-tests), were given two tests (test 1 and test 2). Between test 1 and test 2, half the students received extra tutoring, and half did not. We are interested to learn if the grades of those students who received extra tutoring increased more than for those students who did not receive extra tutoring.
An Example
The dataset used in this example is adapted from the chico dataset in the lsj-data Dat Library. If you want to adapt it yourself, you can simply create a fourth variable in the dataset, called Tutoring. Students 1 through 10 should be given a score of 0 (no tutoring) and Students 11 through 20 should be given a score of 1 (tutoring). The first few rows of your datafile will then look like this:
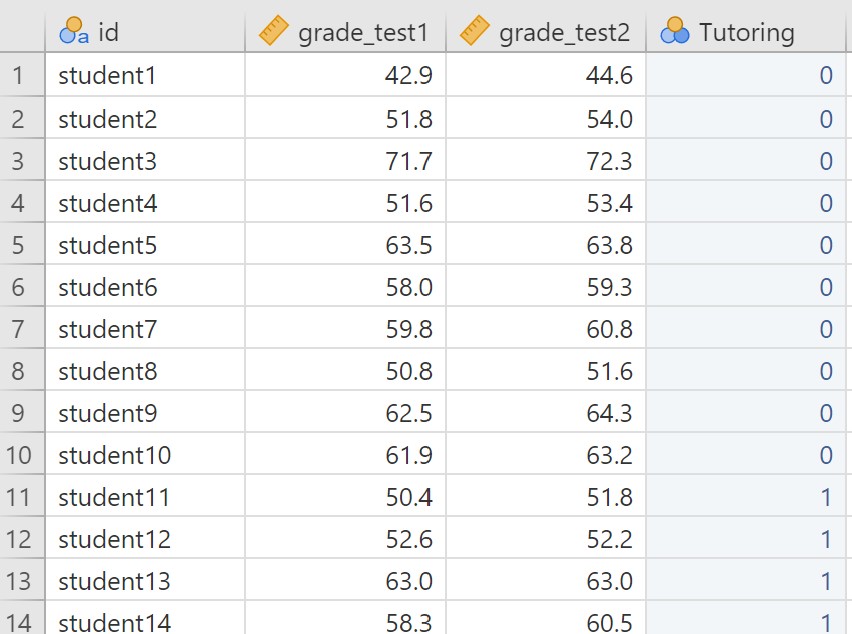
In this dataset, we know have one within-subjects factor (testing occasion: test one or test two) and one between-subjects factor (tutoring: no tutor or tutor). Therefore, it is a mixed design. Let’s suppose that we hypothesize a main effect of testing occasion (scores should increase from test one to test two) and an interaction (students who had a tutor should show a greater increase in test scores from test 1 to test 2 than students who did not have a tutor).
To run a mixed ANOVA in jamovi, after selecting ANOVA, select Repeated Measures ANOVA – use Repeated Measures ANOVA for any situation where you have at least one within-subjects factor. Enter your levels of the within-subjects variable as you did for the repeated measures ANOVA in chapter 7. Tutoring will then go in the Between Subjects Factors box. Choose Generalised η2 as the measure of effect size and type Grade in the Dependent Variable Label box. Select all the assumption checks (you need to check assumptions for both the between- and the within-subjects factor!).
Why did I get “NaN” for Mauchly’s test of sphericity? Sometimes you will get a value of “NaN” for the p-value for the test of sphericity. This will occur when we only have two levels of our within-subjects factor (as in the example above: test 1 and test 2). The test of sphericity works by looking at the differences among the differences in the variances, but when we only have two levels, there is only one difference to be examined, so we cannot get a value for Mauchly’s. In fact, in those situations, there is no point running this test, but I wanted you to do it here so that you could see what happens.
Select Post Hoc Tests for the interaction term, applying No correction. We had predicted an interaction and so we will treat these post hoc tests as planned comparisons and apply the Bonferroni correction ourselves, assuming the interaction term in the ANOVA is significant. You can also obtain the estimated marginal means for both main effects and the interaction term.
Let’s look at the results. Because we have both a within- and a between-subjects factor, we need to look for both of those results in the output. This is a two-way ANOVA, so we should be looking for two main effects and one interaction. Even though we did not hypothesize a main effect of tutoring, we are still going to report both main effects and the interaction when we write up our results (whether significant or not).
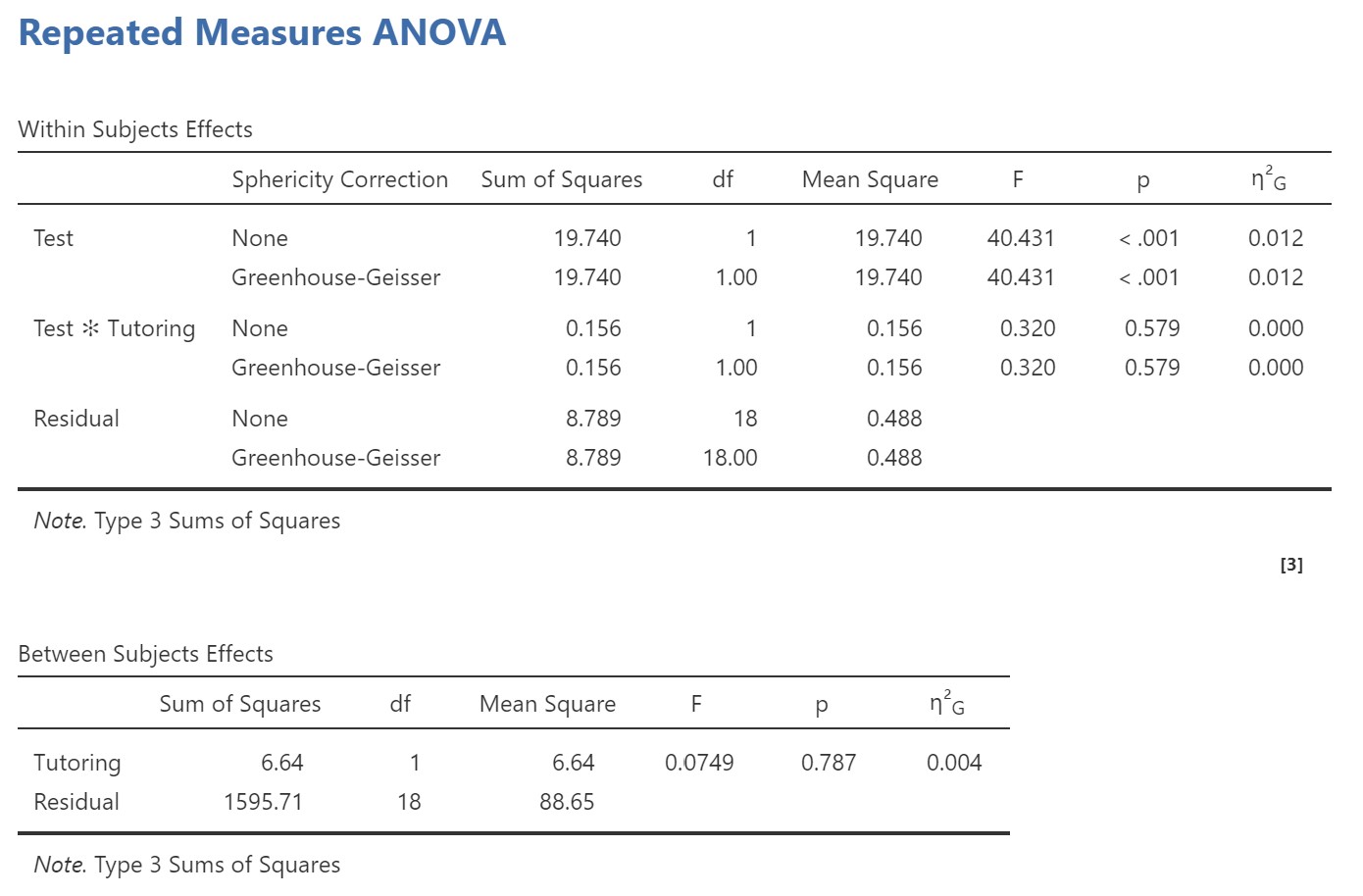
You’ll see that the Within Subjects Effects table shows you the statistics for any test that included at least one within-subjects factor (i.e., the main effect of test, and the interaction between test and tutoring). The Between Subjects Effects table shows you the statistics for any test that includes only between-subjects factor(s) (i.e., the main effect of tutoring). Therefore, if we had another between-subjects factor (e.g., student’s major: Psychology or History), the main effect of major would also appear in the Between Subjects Effects table, as would the interaction between major and tutoring. On the other hand the interaction between major and test, and the three-way interaction between tutoring, major and test, would appear in the Within-Subjects Effects box (because that contains any effects that include at least one within-subjects factor!).
We can see that there was a significant main effect of test, but no significant effect of tutoring and no significant interaction. Because the interaction was not significant, we do not follow up with our planned comparisons. Our results section would look something like this (remember to report all main effects and interactions, whether significant or not).
I used mixed ANOVA to examine the effects of test and tutoring on students’ grades. Students grades improved significantly from test 1 (M = 57.0, SE = 1.52, 95% CI [53.8, 60.2]) to test 2 (M = 58.4, SE = 1.47, 95% CI [55.3, 61.5]), F(1, 18) = 40.43, p < .001, η2G = .012. However, there was no main effect of tutoring (no tutor: M = 58.1, SE = 2.11, 95% CI [53.7, 62.5]; tutor: M = 57.3, SE = 2.11, 95% CI [ 52.9, 61.7]), F(1, 18) = 0.07, p = .79, and no significant interaction between tutoring and testing occasion, F(1, 18) = 0.32, p = .58.
Note
When using repeated measures ANOVA, there is no option to get Cohen’s d for our post hoc tests, should we need them for breaking down significant main effects or an interaction. There are several different ways to get Cohen’s d via jamovi, or, you can use the following approach. For between-subjects comparisons, use the t and n for each group as follows:
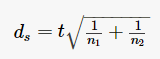
For within-subjects comparisons, use the mean difference and the standard deviation for each level of interest (obtained by running descriptive statistics through Exploration in jamovi), as follows:
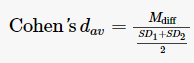
(see Lakens, 2013, for more discussion of appropriate calculations for Cohen’s d)
