26 Theory of One-Way Repeated Measures ANOVA

MS_m and MS_r are computed slightly differently from in the one-way ANOVA (between-subjects). Specifically, the variance is partitioned as follows:

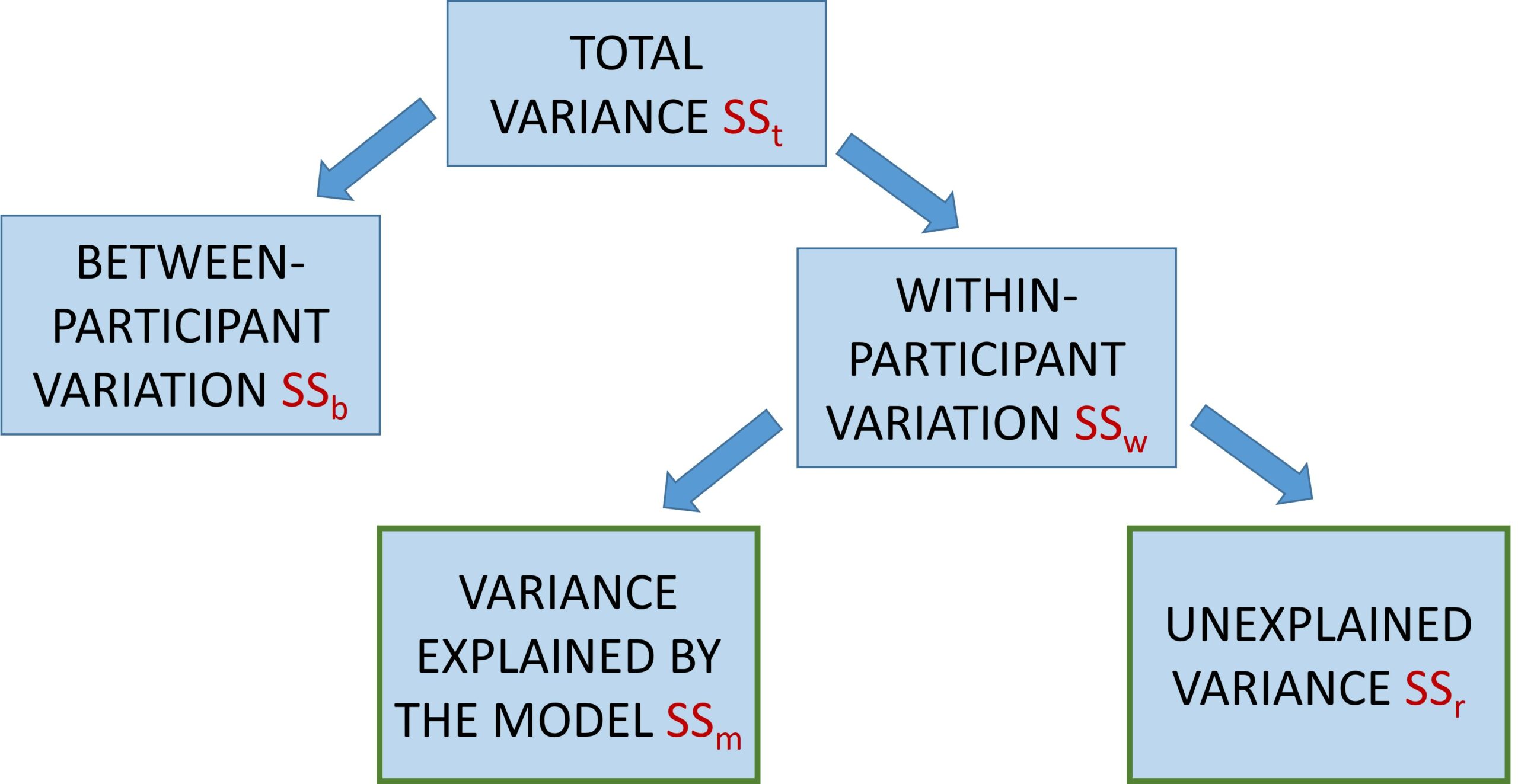
Within-participant variation is decomposed into two types of variance. Our experimental effect (our model sum of squares – variance explained by the model) is now part of the within-participant variation, because all participants complete all conditions in the experiment. So, some of the variability within participants is due to our manipulation of the independent variable (SS_m) and some of it is due to random variation within participants over the levels of the independent variable (SS_r – “error”).

Without getting into the calculations for each of these types of variance, they can be described as follows:

• SS_t – variability of scores around the grand mean in the experiment
• SS_w – variation of individual participant scores
• SS_m – variation of level means around the grand mean
• SS_r – how much variation cannot be explained by the model

The one-way repeated measures of ANOVA, like the one-way ANOVA (between-subjects) that you learned about in the previous chapter, then uses the following equation for the F-ratio (where MS = SS/df):